En microminéralogie on n'a souvent qu'une vision partielle des cristaux (au fond d'une géode), il peut donc être utile de vérifier avec précision les quelques angles visibles pour valider une modélisation, voir l'identification du minéral.
Voici une application Excel qui calcule tous les angles relatifs à une partie de cristal : une face centrale (F) et ses faces adjacentes ou voisines (f1, f2...jusqu'à 12), à partir des paramètres de la maille et des indices de Miller: valeurs goniométriques, angles aux sommets et angles entre faces.
Les plus utiles sont, en vue perpendiculaire à F, les angles aux sommets (angles réels pour F et angles apparents pour les autres)
Exemple avec une allanite/dissakisite de Trimouns (les modélisations sont faites avec le logiciel FACES)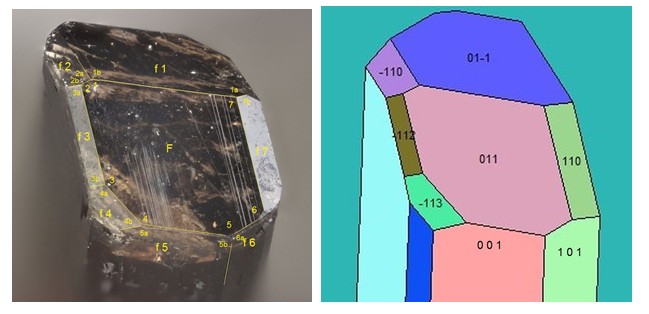
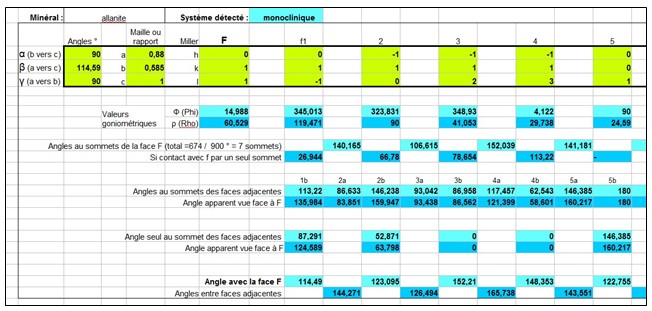
L'utilisation est très simple, saisie dans les cellules vertes, résultats des calculs dans les bleues :
Par exemple on a au niveau du sommet n°3 de F les angles suivants (calculés/mesurés) :
F3 : 152,039 / 150,9° 3b : 86,562 / 86,7° 4a : 121,399 / 122,5°
L'écart atteint fréquemment 1 voir 2 degrés, au delà il faut vérifier la modélisation.
Nb : la méthode pour estimer les angles sur un image et le mode d'emploi complet se trouvent dans l'application.
Cliquer ici pour télécharger l'application au format Excel
Cette application s'ouvre aussi avec Open Office
Autre exemple :
Une question récurrente revient sur l'interprétation des faces hexagonales de minéraux cubiques (fluorine, galène, pyrite...), s'agit t'il :
- de troncatures du cube aux sommets (1 1 1) le faisant évoluer vers l'octaèdre ?
- de troncatures du cube aux arêtes (1 1 0) le faisant évoluer vers le rhombododécaèdre ?
Une bonne vision d'ensemble permet de trancher : dans le premier cas chaque face hexagonale est bordée de trois faces hexagonales et trois faces carrées, dans le deuxième chaque face hexagonale est bordée de quatre faces hexagonales et de deux faces carrées.
Quand ce n'est pas bien visible, il y a un critère: les angles de la face hexagonale ne sont pas les mêmes :
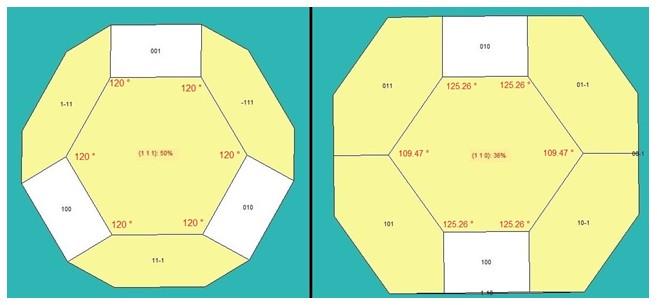
Donc même si on ne voit qu'une face hexagonale, voire un seul angle au sommet, le problème peut être résolu.
Michel Bretheau


