Eric Naud (AFM)
Au départ, je m'étais dit que je n'utiliserais pas le mot symétrie dans mon exposé, afin de simplifier au maximum (l’article faisait alors cinq pages…). Malheureusement pour vous, j'ai échoué, et après réflexion, il n’est pas possible de faire de la cristallographie sans aborder cette notion. Mais je vais quand même essayer d'élaguer un peu.
Même sans rien connaître aux mathématiques, tout le monde sait plus ou moins que la symétrie est la répétition de formes selon des lois géométriques. Présenté comme ça, ça a l'air impressionnant, mais en fait, le principe est assez simple ; c'est son écriture qui prend parfois des formes cabalistiques (par exemple, la symétrie d'un cristal quadratique très banal sera notée « A4, M2A2, 2M', 2A''2, 2M'', C »). Pas de panique, vous n'avez pas l'utilité de ce genre de chose dans l'immédiat. Par contre, la lecture du chapitre ci-dessous est absolument indispensable.
A retenir impérativement :
Dans un cristal, la symétrie peut se manifester de trois manières différentes : plan de symétrie, axe de symétrie, et centre de symétrie.
1- Centre de symétrie :
C'est l'élément de symétrie le moins facile à saisir.
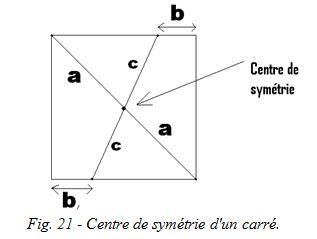
Nous allons d'abord raisonner en deux dimensions. Prenons un carré (fig. 21), et matérialisons son centre par un point. Traçons une ligne partant d'un sommet, et passant par ce centre : à égale distance (notée a sur le schéma ci-dessous) de l'autre côté, nous trouverons le sommet opposé.
Si l'on fait partir la ligne d'un point situé sur un côté à une certaine distance (b sur le schéma) d'un sommet, toujours en passant par le centre, elle recoupera le côté opposé à égale distance c du centre, et en un autre point situé à la même distance b du sommet opposé. Ceci est valable pour tous les points du carré : on dit que le centre du carré est son centre de symétrie.
Plus généralement, on peut dire qu'une figure possède un centre de symétrie si à chaque point de la figure correspond un autre point situé de l'autre côté de ce centre, et à égale distance de celui-ci.
Par conséquent, chaque caractéristique de la figure va se retrouver de l'autre côté du centre de symétrie : chaque angle va avoir son homologue opposé de même valeur, et chaque côté aura son homologue, de même longueur et de même orientation. Autrement dit, la présence d'un centre de symétrie implique que les côtés seront tous parallèles deux à deux.
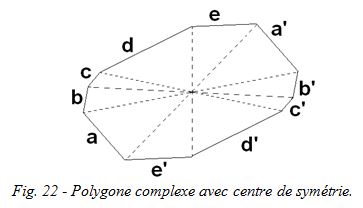
Ainsi, dans la figure ci-dessous, les côtés a et a' sont parallèles et de longueur égale, de même que b et b', c et c', d et d', e et e', et tous les angles qui se font face sont égaux. Le centre de symétrie est là où toutes les diagonales se croisent.
Si l'on passe à la géométrie en trois dimensions, à chaque face de la figure correspond une face symétrique, parallèle mais inversée. De même, à chaque arête correspond une arête symétrique, parallèle et de même longueur, de l'autre côté de la figure.
2-Axe de symétrie :
Ce mode de symétrie n'est pas très difficile à comprendre, mais il est parfois délicat de repérer sa présence dans les cristaux. Il est néanmoins important de bien maîtriser cette notion, qui sera très utile pour identifier en particulier les systèmes quadratique, rhomboédrique, et hexagonal.
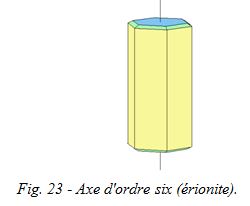
Prenons le cristal d'érionite ci-dessous :
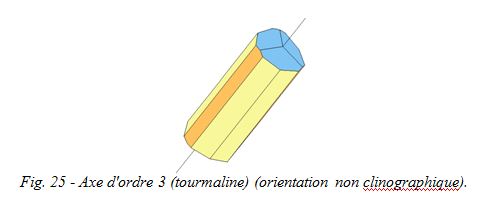
Qui dit axe dit rotation : faisons tourner ce cristal d'un sixième de tour (60°) sur son axe vertical (celui traversant les deux bases hexagonales). On constate que les positions de départ et d'arrivée se superposent exactement. On peut effectuer six fois cette opération, ce qui nous ramène à la position d'origine. On dit que cet axe est un axe de symétrie d'ordre six.
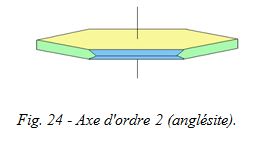
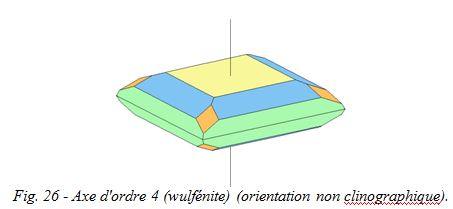
Si au lieu de faire un sixième de tour, il fallait faire un quart de tour pour retrouver une position semblable à celle de départ, on parlerait d'un axe d'ordre quatre. Idem pour un demi-tour (axe d'ordre deux), ou pour un tiers de tour (axe d'ordre trois).
Attention : quand on parle de superposition, il s'agit de superposition complète. Reprenons le dessin du cristal d'érionite : si par exemple il manquait une face pyramidale sur deux (faces vertes sur le dessin), le contour hexagonal du cristal ne suffirait pas pour pouvoir dire qu'il s'agit d'un axe d'ordre six. L'axe serait alors d'ordre trois.
Notez également que, pour d'obscures raisons mathématiques, il n'y a jamais d'axes d'ordre cinq ou supérieur à six dans les cristaux.
Petit exercice pratique : reprenez les collages, et essayez de retrouver tous leurs éléments de symétrie (axes, miroirs, centres).
Si vous êtes observateur, vous devez obtenir les chiffres suivants :
- système cubique : 3 axes d'ordre quatre, 4 axes d'ordre trois, 6 axes d'ordre deux, 9 miroirs, 1 centre.
- système quadratique : 1 axe d'ordre quatre, 4 axes d'ordre deux, 5 miroirs, 1 centre.
- système orthorhombique : 3 axes d'ordre deux, 3 miroirs, 1 centre.
- système monoclinique : 1 axe d'ordre deux, 1 miroir, 1 centre.
- système rhomboédrique : 1 axe d'ordre trois, 3 axes d'ordre deux, 3 miroirs, 1 centre
- système triclinique : 1 centre
- système hexagonal : 1 axe d'ordre six, 6 axes d'ordre deux, 7 miroirs, 1 centre
Vous pouvez également vous entraîner avec les objets de votre quotidien, en cherchant les éléments de symétrie d’une table, d’une roue de voiture, de votre trimmer, etc… Vous acquerrez ainsi au fil du temps la capacité d’identifier rapidement la présence de ces caractères dans un cristal.
3-Plan de symétrie :
C'est facile, c'est un miroir. On dit qu'un cristal possède un plan de symétrie si on peut le couper en deux moitiés telles que l'une soit le reflet de l'autre dans un miroir. Illustration pratique par une manipulation simple : prenez un objet, de préférence de forme géométrique (un fond de boîte micro, par exemple), et plaquez-le contre un miroir. Vous voyez à présent un objet deux fois plus grand, divisé en deux parties égales par le plan de symétrie que constitue le miroir. Rappelez-vous également l'octaèdre en apéricubes sur le miroir.
Voici d'autres exemples simples :
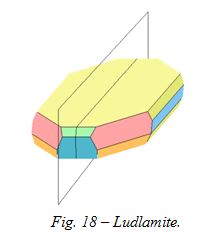
Cette ludlamite (monoclinique) est coupée en deux moitiés semblables par un plan de symétrie (fig. 18).
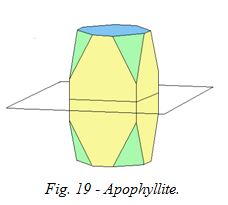
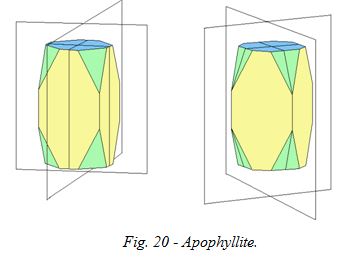
Ce cristal quadratique d'apophyllite comporte plusieurs plans de symétrie : on peut le couper à mi-hauteur parallèlement aux bases (fig. 19), mais aussi verticalement (fig. 20), en passant soit par les milieux des faces latérales (faces jaunes sur le schéma), soit par les milieux des faces pyramidales (faces vertes).
Notre apophyllite possède donc en tout cinq plans de symétrie.
4-Classe de symétrie :
Nous venons de voir que chaque système cristallin possède un certain nombre d'éléments de symétrie. Il s'agit cependant d'un nombre maximum : tous ces éléments ne sont pas obligatoirement présents dans un cristal. Pourquoi ? Parce que je vous ai menti dès le début. Même si à l'échelle macroscopique, et même microscopique, chaque cristal appartient obligatoirement à l'un des sept systèmes cristallins, le nombre de formes possibles de la maille primitive est bien plus considérable. Un clair dessin valant mieux qu'un long baratin, examinons les schémas ci-dessous :
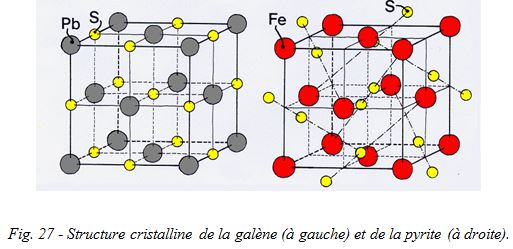
Dans la galène, la maille primitive est très simple : elle est constituée d'une alternance d'atomes de plomb et de soufre bien alignés sur des rangées se coupant à 90°. Chaque atome de plomb est entouré de six atomes de soufre, et réciproquement. La symétrie est « maximum » : observez-la bien, vous retrouverez tous les éléments de symétrie du cube.
La structure de la pyrite, par contre, est beaucoup plus complexe. Les atomes de fer dessinent bien une maille cubique semblable à celle des atomes de plomb dans la galène, mais les atomes de soufre ne sont pas disposés de la même manière : ils sont situés sur les diagonales des huit petits cubes constituant le cube principal, à 1/5 d'une de leurs extrémités (oui, il m'a fallu un moment, à moi aussi...). Non seulement leur répartition différente va modifier le comportement chimique du cristal, et donc sa croissance, mais la plus faible symétrie de la maille va se retrouver à l'échelle macroscopique, ce qui va se traduire par la disparition de certaines faces.
La présence ou l'absence de certains éléments de symétrie déterminent en fait, au sein des sept systèmes cristallins, les trente-deux classes de symétrie qui intriguent tant le débutant. Vous n'êtes pas obligé de les apprendre toutes : certaines d'entre elles sont extrêmement rares dans la nature, et de toutes façons, la liste complète figure dans tous les bons manuels (et même dans les mauvais...).
Entraînez-vous par contre à mémoriser les plus courantes : reconnaître non seulement le système cristallin d'un minéral, mais également sa classe de symétrie, peut constituer une aide précieuse pour son identification. Démonstration :
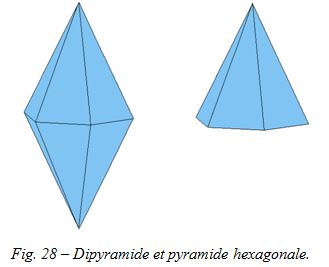
Prenons un cristal hexagonal, mais présentant uniquement les faces pyramidales. Si la maille appartient à la classe ayant le degré de symétrie le plus élevé, le cristal apparaît ainsi (fig. 28 gauche) :
C’est une dipyramide. Il comporte notamment un miroir horizontal passant par le milieu du cristal, c'est-à-dire par la base commune aux deux pyramides. Il n’est pas dessiné sur la figure ci-dessus, mais on le devine aisément.
Si ce miroir n'existe pas (fig. 28 droite), on supprime du même coup le reflet de la moitié supérieure (ou inférieure, si vous préférez). Le cristal devient une simple pyramide hexagonale. L'aspect a radicalement changé (six faces pyramidales au lieu de douze, et une base hexagonale), et pourtant c'est toujours un cristal dérivant d'un prisme droit à base hexagonale.
Or parmi les sept classes de symétrie du système hexagonal, deux seulement peuvent aboutir à des cristaux de ce type. Vous venez de bien déblayer le chemin de son identification. Si par exemple vous êtes à Carrare, dans les célèbres carrières de marbre, vous venez sans doute de trouver un très beau cristal de wurtzite.
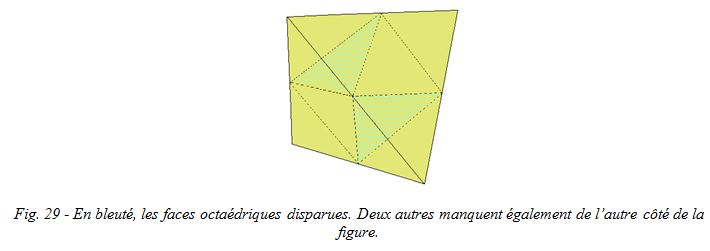
Reprenons notre octaèdre de tout à l'heure : pour l'obtenir, nous avons tronqué un cube possédant tous les éléments de symétrie du système cubique. Si dans ce cube on supprime certains éléments de symétrie, en particulier les axes d'ordre quatre, trois miroirs et le centre, seule la moitié des faces de l'octaèdre va apparaître. Les mêmes troncatures donneront un cristal non pas octaédrique, mais tétraédrique (fig. 29).
Ce n'est pas clair ? C'est normal. Mettez ça de côté, et revenez-y demain. Puis après-demain. Puis la semaine suivante, et celle d'après aussi. Autant que je me souvienne, il a dû me falloir environ six ans pour comprendre le fonctionnement du tétraèdre... Ferez-vous mieux ?